Каждый, кто хоть раз думал в своей жизни о том, как стать "профи" или "системный администратор", а просто, чтобы связать судьбу вычислительной техники, знания о представлении числа в памяти компьютера, что является абсолютно необходимым. Потому что он на основе этого языки программирования низкого уровня ассемблер. Поэтому сегодня мы рассмотрим представления чисел в компьютерах и их размещение в ячейках памяти.
Системы счисления
 Вам будет интересно:Дизайн презентации: советы по созданию
Вам будет интересно:Дизайн презентации: советы по созданию
Если Вы читаете эту статью, вы, вероятно, уже знаете это, но стоит повторить. Все данные в персональном компьютере хранится в двоичном формате. Это означает, что все числа должны быть представлены в соответствующей форме, которая состоит из нулей и единиц.
Чтобы перевести для нас обычные десятичные числа в форме, понятной для компьютера, вы должны использовать следующий алгоритм. Есть специальные калькуляторы.
Поэтому, для того, чтобы перевести число в двоичную систему счисления нужно взять выбранное значение и разделить его на 2. Тогда мы получим результат и остаток (0 или 1). Результат снова разделить на 2 и запишите остаток. Эту процедуру следует повторять до тех пор, пока в конце концов не быть 0 или 1. Затем написать конечного значения и остается в обратном порядке, как мы их получили.
Именно так и происходит представления чисел в компьютерах. Любое число, записанное в двоичной системе, а затем занимает ячейку памяти.
 Вам будет интересно:Как получить root права на Android через ПК?
Вам будет интересно:Как получить root права на Android через ПК?

Памяти
Как вы уже должны знать, минимальной единицей информации является 1 бит. Как мы видели, представление чисел в ЭВМ происходит в двоичном формате. Таким образом, каждый бит памяти занимает одна значение, 1 или 0.
Используется для хранения большого количества клеток. Каждый блок содержит до 8 бит. Таким образом, можно сделать вывод, что минимальное значение в каждом из сегментов памяти может быть 1 байт или восемь-значное двоичное число.
Весь
Наконец мы добрались до непосредственного размещения данных на компьютер. Как уже упоминалось, первое, что процессор преобразует информацию в двоичном формате, а потом помещает их в память.
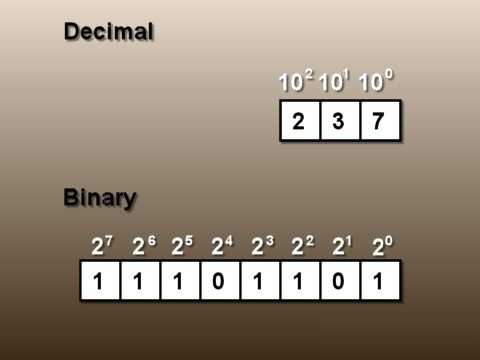
Мы начнем с самого простого варианта, который является представлением целых чисел в компьютере. ПК отводит под этот процесс до смешного малое количество клеток – только один. Таким образом, максимум в один слот может иметь значение от 0 до 11111111. Давайте переведем максимальное число в обычной форме.
Х = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
Теперь мы видим, что в одной ячейке памяти может иметь значение от 0 до 255. Однако, это применимо только для неотрицательных целых чисел. Если компьютер нужно записать отрицательное значение, все пошло бы по-другому.

Отрицательные числа
Теперь давайте посмотрим, как представление чисел в компьютере, если они отрицательные. Для размещения значений, которые меньше нуля, присваивается две ячейки памяти, или 16 бит информации. В то время как 15 пройти под само число, а первый (левый) бит отводится под соответствующий знак.
Если цифра отрицательная, то записывается "1" в случае положительного результата "0". Для простоты запоминания можно провести аналогию: если знак есть, то ставим 1, если нет, то ничего (0).
Остальные 15 бит, отведенных на номер. Аналогично предыдущему случаю, они могут разместить максимум пятнадцати единиц. Следует отметить, что учет отрицательных и положительных чисел значительно отличаются друг от друга.
Для того, чтобы разместить 2 ячейки памяти значение больше или равно нулю, так называемый прямой код. Эта операция выполняется точно так же, как было описано, и максимум = 32766 при использовании десятичной системы счисления. Сразу хочу отметить, что в данном случае "0" относится к положительной.
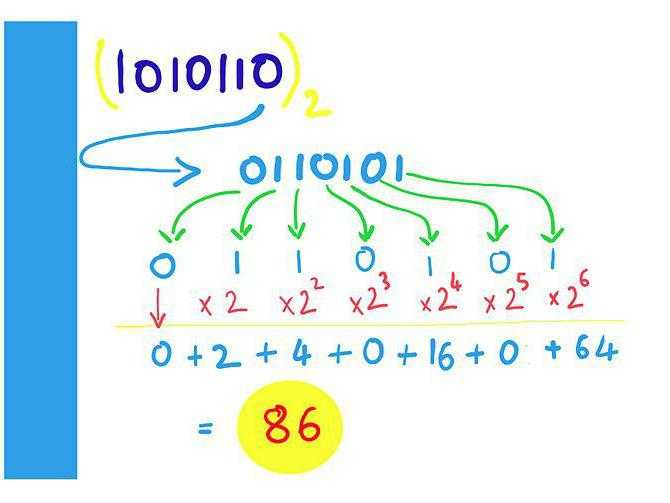
Примеры
Представление целых чисел в памяти компьютера-это не такая сложная задача. Хотя это немного более сложным, если он является отрицательной величиной. Чтобы записать число, которое меньше нуля, использовать дополнительный код.
Чтобы сделать это, машина производит ряд вспомогательных операций.
Рассмотрим пример. Пусть у нас есть число X = - 131. Во-первых, получить модуль |х|= 131. Потом перевести в двоичную систему и записать в 16 клеток. Получишь Х = 0000000010000011. После инвертирования х=1111111101111100. Добавить к нему "1" и получить обратный код X=1111111101111101. Для записи в 16-битном минимальный номер ячейки памяти-это x = - (215) = - 32767.
Длинных целых чисел
Как видите, представления действительных чисел в компьютерах не так сложно. Однако, в рассматриваемом диапазоне не может быть достаточно для большинства операций. Поэтому, для того, чтобы вместить большое количество, что компьютер выбирает 4 ячейки памяти, или 32 бита.
Процесс записи абсолютно не отличается от представленного выше. Итак, мы просто даем диапазон чисел, которые могут храниться в этом типе.
Hmag=2 147 483 647.
ГМЗ=- 2 147 483 648.
Эти ценности, в большинстве случаев, для того, чтобы записывать и проводить данные операции.
Представление вещественных чисел в компьютере имеет свои преимущества и недостатки. С одной стороны, эта техника облегчает выполнение операций между целочисленными значениями, что значительно ускоряет работу процессора. С другой стороны, этот диапазон оказывается недостаточным для решения большинства задач экономики, физики, арифметики и других наук. Поэтому теперь мы рассмотрим другой способ для холуйства.
С плавающей точкой
Это последнее, что вам нужно знать о представлении чисел в компьютере. Потому что при написании дроби, возникает проблема определения положения запятой в них, чтобы расположить эти числа в компьютере используется экспоненциальная форма.
Любое число может быть представлено в следующем виде X = м * РП. Где m-мантисса, Р системы счисления, а n – экспонента.
Для стандартизации записи чисел с плавающей запятой, используйте следующее условие, при котором модуль мантиссы должна быть больше или равна 1 и меньше 1.
Пусть нам дано число 666,66. Привести его в экспоненциальной форме. Получишь Х = 0,66666 * 103. П = 10 и П = 3.
Для хранения значений с плавающей точкой, обычно это 4 или 8 байт (32 или 64 бит). В первом случае она называется число обычной точности, а второй-с двойной точностью.
Из 4 байтов, выделенных для хранения цифр 1 (8 бит) приведены данные о заказе и его знак, и 3 байта (24 бита) для хранения мантиссы и ее знака по тем же принципам, как и для целочисленных значений. Зная это, мы можем сделать некоторые простые вычисления.
Максимальное значение P = 11111112 = 12710. Исходя из этого, мы можем получить максимальный размер целого числа, которое может храниться в памяти компьютера. Х=2127. Теперь мы можем рассчитать максимально возможную мантиссу. Она будет равна 223 – 1 ≥ 223 = 2(10 × 2,3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107. В конце концов, мы получили приблизительное значение.
Теперь, если мы объединим оба вычисления, мы получим значения, которые могут быть записаны без потери в 4 байта памяти. Он равен х = 1,701411 * 1038. Остальные цифры были отброшены, потому что такая точность делает возможным такой способ записи.
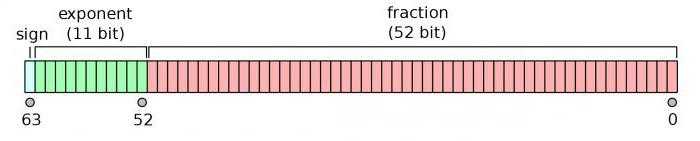
Двойной точности
Поскольку все расчеты были уточнены и объяснены в предыдущем пункте, здесь мы очень коротко расскажем вам все. Для чисел с двойной точностью обычно отводится 11 разрядов для порядка и его знака, и 53 бита мантиссы.
Н = 11111111112 = 102310.
М = 252 -1 = 2(10*5.2) = 10005.2 = 1015.6. Сгоняли и получить максимальное число х = 21023 до "М".
Надеюсь, информация о представлении целых и вещественных чисел в компьютере, который мы предоставили будет полезно для вас в обучении и станет хоть немного яснее, чем то, что обычно пишут в учебниках.
