Элементарные логические операции в информатике

Содержание статьи:

Отказ
Дополнение
Умножение
Результат
Равенство
Свойства
Заключение

Каждый, кто начинает изучать информатику, выучить двоичную систему. Он используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если подумать, то они используются при создании логики вычислительных машин и оборудования.

Отказ

Прежде чем начать подробно рассматривать конкретные примеры, мы перечислим основные логические операции в информатике:

логические операции в информатике

отрицание;
дополнение;
умножения;
следующее;
равенства.

Вам будет интересно:Что такое дополненная реальность? Дополненная реальность

Перед началом исследования логических операций стоит сказать, что в информатике ложь обозначается "0" и правда является "1".

Для каждого действия, как и в обычной математике, мы используем следующие логические операторы в компьютерные науки: , в, &, ->.

Каждое действие описывается или цифры 1/0, или просто логических выражений. Мы начинаем с простейших математических логических операций, используя только одну переменную.

Логическое отрицание-операция инверсии. Суть в том, что если исходное выражение истинно, то результат инверсии-это ложь. И наоборот, если исходное выражение ложно, то результат инверсии будет правдой.

При написании этого выражения используется следующее обозначение "А".

Дать таблицу истинности - схема, которая показывает все возможные результаты операции в любом из исходных данных.

Таблица истинности для инверсии

И	х	на
А	на	х

То есть, если у нас есть исходное выражение истинно (1), то его отрицание ложно (0). Но если исходное выражение ложно (0), то его отрицание истинно (1).

Дополнение

Остальные операции требуют двух переменных. Обозначим одно выражение - 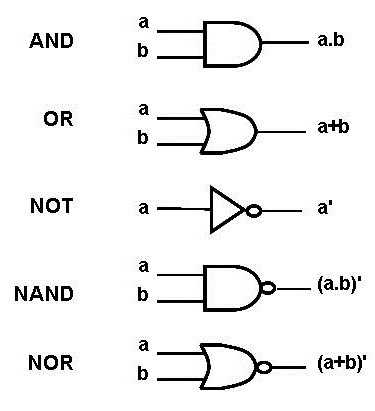информатика свойства логических операций и во втором веке логических операций в информатике, обозначающий действие сложение (или, дизъюнкция), при записи обозначаются слову "или" или символ "Х". Выписать возможных вариантов и результатов расчета.

Е=1, N=1 ,то Е В Н = 1. Если оба выражения имеют значение true, то их дизъюнкция-это тоже правда.

Е=0, Н=1 ,в конце концов, е V Н = 1. Е=1, n=0 , тогда Е В Н= 1. Если хотя бы одно из выражений имеет значение true, то результатом их сложения должны быть правдой.

Е=0, n=0 ,то результат Е В Н = 0. Если оба выражения ложны, то их сумма тоже ложь.

Для краткости, давайте создадим таблицу истинности.

Дизъюнкция

Е	х	х	на	на
Н	х	на	х	на
Е В Н	х	х	х	на

Умножение

Покончив с операцией сложения, двигаясь на умножение (конъюнкция). Мы используем те же обозначения, приведенные выше, для того. При написании логическое умножение обозначается значком " & " или "J".

Е=1, N=1 ,то Е & П = 1. Если оба выражения имеют значение true, то их соединение является истиной.

Если хотя бы одно из выражений ложно, то в результате логического умножения тоже будет ложью.

Е=1, н=0, так что Е и Н = 0.
Е=0, N=1, то Е & П = 0.
Е=0, n=0, то результат Е & П = 0.

Вместе

Е	х	х	0
Н	х	0	х
Е И Н	х	0	0

Результат

Логической последовательности (импликация) - это один из самых простых в математической логике. Оно базируется на одной аксиоме истины, чтобы следовать ложь.

Е=1, ч=, следовательно, Е -> П = 1. Если пара в любви, они могут целовать правду.

Е=0, N=1, то Е -> Н = 1. Если пара не влюблены, они могут поцеловать тоже может быть правдой.

Е=0, н=0, из этого Е -> Н = 1. Если пара не в любви, они не целуются - тоже правда.

Е=1, n=0, то результатом является Е -> Н = 0. Если пара в любви, они не целуются-это ложь.

Чтобы облегчить выполнение математических операций, также дать таблицу истинности.

Импликация

Е	х	х	на	на
Н	х	на	х	0
Е -> Н	х	на	х	х

Равенство

Вчера пересмотрел операции будут идентичны логического равенства или эквивалентности. В тексте она может именоваться "...тогда и только тогда, когда...". Исходя из данной формулировки, мы пишем примеры на все варианты источник.

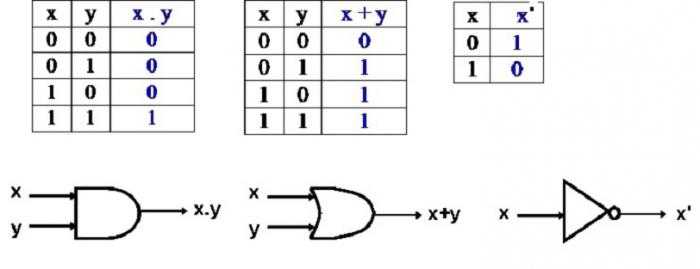
основные логические операции в информатике

А=1, B=1, то а≡в = 1. Людей на таблетки, если и только если заболеет. (правда)

А=0, Б=0, в результате≡в = 1. Человек не на таблетки тогда, и только тогда, когда не больны. (правда)

А=1, b=0, так что а≡в = 0. Людей на таблетки, если и только если это не больно. (ложь)

А=0, Б=1 ,то а≡в = 0. Человек не на таблетки, а потом только когда больно. (ложь)

МФЛ

И	х	на	х	на
В	х	на	0	х
А≡В	х	х	на	на

Свойства

Так, после рассмотрения элементарных логических операций в информатике, мы можем приступить к изучению некоторых их свойств. Как в математике, логические операции, существует порядок обработки. В большие логические выражения, операции в скобках выполняются в первую очередь. После того, как они сначала вычислить все значения отрицания в пример. Следующий шаг-это расчет вместе, затем дизъюнкция. Только после этой операции следствия и, наконец, равнозначность. Рассмотрим небольшой пример.

И V & К - > ≡ в

Процедура следующие.

В&(Б)

И V(В&(В))

(А V(В&(В)))->

((И V(В&(В)))->В)≡А

Для того, чтобы решить этот пример, мы должны построить расширенную таблицу истинности. Создавая ее, помните, что лучше иметь столбцы в том же порядке и будет выполнять действия.

Образец решения

И	В	В	В&(Б)	И V(В&(В))	(А V(В&(В)))->	((И V(В&(В)))->В)≡А
х	на	х	на	х	х	х
х	х	на	на	х	х	х
на	на	х	на	на	х	на
на	х	на	на	на	х	на

Как мы видим, результат решения примера будет последней колонке. Таблица истинности помогли решить проблему с любым исходным данным.

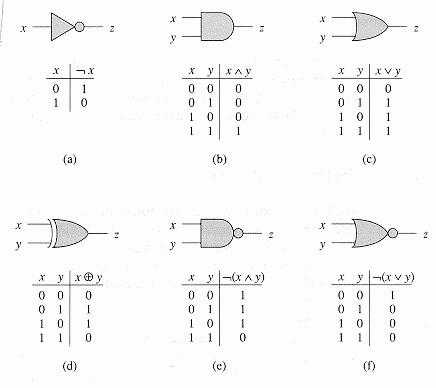
знаки логических операций в информатике

Заключение

В этой статье мы рассмотрели некоторые понятия математической логики, таких, как информатика, свойства логических операций, а также то, что логические операции сами по себе. Были даны некоторые простые примеры для решения задач математической логики и таблицы истинности, для того, чтобы упростить этот процесс.

Источник